Dynex solidifies its leadership in quantum computing, reaching a groundbreaking milestone in Quantum Volume

Quantum Volume allows for fair comparisons between different platforms and gives a clear indication of a system’s scalability and potential to tackle real-world problems. Dynex has set a new global benchmark by achieving a Quantum Volume of 2¹¹⁹ , exponentially surpassing its closest competitors and pushing the boundaries of the quantum ecosystem to unprecedented levels.

Dynex is announcing another milestone, a thirty-one-figure Quantum Volume (QV) of 2¹¹⁹ — reinforcing our commitment to building, by a significant margin, the highest-performing quantum computing system in the world. This is orders of magnitude higher than the previously reported record of 2²⁰ set by competitors on April 16th, 2024.

As the quantum computing industry continues to evolve, measuring the performance and progress of quantum systems becomes crucial. Traditional metrics such as qubit count, while useful, do not provide a complete picture of a quantum computer’s practical capabilities. This is where Quantum Volume (QV) comes into play. Developed by IBM, QV is a performance metric that encapsulates multiple aspects of a quantum computer’s abilities into a single number, offering a holistic view of its computational power.

Quantum Volume is important because it goes beyond just the number of qubits. While qubit count has often been cited as a key indicator of a quantum computer’s power, it doesn’t account for other essential factors like gate fidelity, error rates, and circuit depth. Quantum Volume captures all these dimensions, offering a more comprehensive evaluation of a quantum system’s performance. Essentially, QV reflects not just the size of a quantum processor but also how well that processor can execute complex quantum circuits reliably.

Source: Quantum 6, 707 (2022)

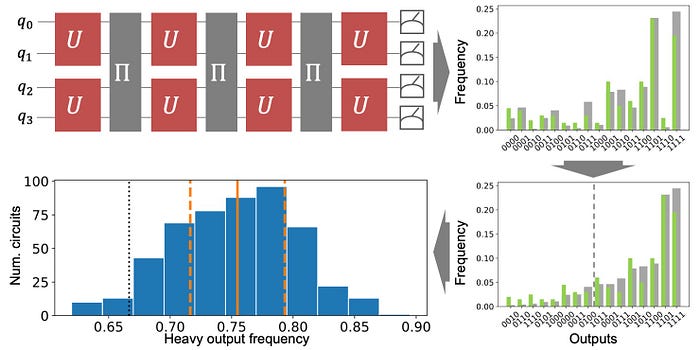
The calculation of Quantum Volume is rooted in a series of random quantum circuits, where the depth of the circuit is set to be equal to the number of qubits. The system’s ability to execute these circuits successfully is tested, and the results are analyzed to determine the probability of producing “heavy outputs” — those whose probabilities are in the upper 50% of the expected theoretical distribution. If the quantum computer can successfully achieve this output with more than two-thirds accuracy, the QV is calculated as 2^n, where n is the number of qubits.

What makes QV especially valuable is its ability to assess quantum scalability. Quantum computers are subject to a range of errors, from gate imperfections to decoherence and noise, which make it difficult to execute circuits as they grow in size and depth. A system with a high QV demonstrates that it can handle large, complex quantum circuits without significant degradation in performance. In this way, QV provides a clear picture of how well a quantum computer can scale and maintain its reliability as problems become more complex.

Quantum Volume also offers a standardized metric for comparing different quantum architectures and platforms. As various quantum computing technologies — such as superconducting qubits, trapped ions, and photonic qubits — compete to dominate the field, QV serves as a neutral benchmark. By measuring QV across different systems, researchers and developers can more accurately compare progress and innovation across platforms, moving beyond just qubit count to consider real-world performance.

The implications of Quantum Volume are broad, especially for the future of practical quantum applications. Quantum systems with higher QV are better equipped to solve more complex problems, such as those found in cryptography, optimization, material science, and drug discovery. These are areas where classical computers struggle, and where quantum computers are expected to outperform as they mature. Increasing a system’s QV is critical to unlocking the true potential of quantum computing, as it demonstrates the ability to handle more complex algorithms and workloads.

The Neuromorphic Quantum Computing Advantage

A traditional quantum computer leverages quantum-mechanical phenomena like superposition and entanglement to perform computations. Unlike digital computers, which store data as definite states (0 or 1), quantum computation uses quantum bits (qubits), capable of existing in a superposition of states. Qubits can be implemented using distinguishable quantum states of elementary particles such as electrons or photons. For instance, a photon’s polarisation can represent qubits, with vertical and horizontal polarisation as states, or an electron’s spin, with “up” and “down” spins representing the two states.

Qubits have been implemented using various advanced technologies capable of manipulating and reading quantum states. These technologies include, but are not limited to, quantum dot devices (both spin-based and spatial-based), trapped-ion devices, superconducting quantum computers, optical lattices, nuclear magnetic resonance (NMR) computers, solid-state NMR Kane quantum devices, electrons-on-helium quantum computers, cavity quantum electrodynamics (CQED) devices, molecular magnet computers, and fullerene-based ESR quantum computers. Each of these approaches leverages different physical principles to create and control qubits, contributing to the diverse landscape of quantum computing technologies.

Current quantum computing technology, while promising, faces significant challenges that limit its scalability and practical application. These challenges primarily stem from the limited number of qubits available, the high susceptibility of qubits to errors, and the complexity of error correction protocols necessary to maintain coherence in quantum states. As quantum systems grow in size, the need for sophisticated error correction becomes increasingly critical, further complicating the development of reliable quantum computers.

Given these constraints, there is a growing interest in simulating quantum computers on classical hardware. One of the most promising methods involves reformulating quantum algorithms into their corresponding partial differential equations (PDEs), governed by Schrödinger’s equations. Schrödinger’s equations, which describe the quantum state of a system, provide a theoretical framework for simulating quantum dynamics on classical systems. However, this approach presents its own set of challenges: the computational resources required to solve these PDEs scale exponentially with the size of the quantum system being simulated.

This exponential growth in resource requirements stems from the inherent complexity of quantum systems, where the state space increases exponentially with the number of qubits. Consequently, while the theoretical formulation offers a pathway to simulate quantum algorithms, the practical limitations of classical computational resources pose significant barriers. Overcoming these barriers is crucial for advancing the field of quantum computing and for enabling more accurate and scalable simulations that can bridge the gap between current quantum capabilities and their potential applications.

Dynex’ Neuromorphic Quantum Computing approach enables efficient, large-scale computation of quantum algorithms and circuits on traditional hardware, without sacrificing the fidelity or capabilities of quantum mechanics-based systems, thus bridging the gap between classical and quantum computing paradigms. It allows the reformulation of quantum algorithms into a system of ordinary differential equations (ODEs), which require computational resources that scale only linearly with the size of the quantum system being simulated.

This reformulation of quantum algorithms into ordinary differential equations (ODEs) is crucial because it significantly reduces the computational resources required for quantum simulations. Unlike the traditional approach, where resources scale exponentially, the ODE-based method scales linearly with the size of the quantum system. This improvement allows for the simulation of much larger quantum systems on classical hardware, making it more feasible to explore and develop quantum algorithms. Additionally, it enhances accessibility, enabling broader research and application in quantum computing by reducing the computational overhead.

Dynex’ Global Head of Quantum Solutions Architecture, Samer (Sam) Rahmeh, recently conducted a quantum volume measurement and reached an unprecedented result of 2¹¹⁹. This remarkable accomplishment significantly surpasses previously established records and underscores Dynex’s superior capabilities in quantum computing. The achievement of such a high QV demonstrates the platform’s ability to manage complex quantum circuits efficiently, with enhanced error correction and gate fidelity. This milestone not only validates Dynex’s technological advantage but also positions the platform as a leader in the field of scalable quantum computation. Through this breakthrough, Dynex establishes itself at the forefront of quantum research, advancing the practical application of quantum technologies.

YouTube screen-recording (realtime) of the QV measurement:
https://youtu.be/eEiu8e8xlMo

Dynex’ Quantum Volume on Github:
https://github.com/dynexcoin/DynexSDK/tree/main/QV

Neuromorphic Quantum Computing with Dynex:
https://dynex.co/learn/n-quantum-computing

Learn more about Dynex:
https://dynex.co